M1.D8: Rotational levels of molecules

M1.D8: Rotational levels of molecules#

Learning Objectives#

  • Describing the rigid rotor approximation for the angular solution of quantum nuclear motion of a diatomic molecule. List the energy of rotational levels using the quantum number J.

  • Plotting how the rotational levels are affected by the mass, the bond distance, and the moment of inertia of a diatomic molecule.

  • Applying the rigid rotor model to real diatomic molecules.

  • Discussing and plotting the degeneracy of rotational levels for each quantum number J.

  • Calculating and plotting spectroscopic lines of microwave spectroscopy of diatomic molecules. Listing allowed transitions using the selection rule \(\Delta\)J = \(\pm\) 1.

The Schrodinger equation for nuclear coordinates: the polar coordinates of the nuclear motion show rotation#

The Hamiltonian for the nuclear motion (after we have split the electronic from the nuclear motion) was already written before

\[ \hat{H}_{nuclear} = \sum_{k=nuclei}-\frac{1}{2m_k}\nabla_{k} + U(r) \]

So we have a new differential equation to solve that depends on the nuclear coordinates “xyz” for any molecular system.

\[ \sum_{k=nuclei}-\frac{1}{2m_k}\nabla_{k}\Psi(xyz) + U(r)\Psi(xyz) = E\Psi(xyz) \]

For a non-linear molecule with N atoms, it will have 3N coordinates. Out of these 3N coordinates, 3 will be translations in the xyz directions, 3 more will be rotations, and 3N-6 will be vibrations.

When we solved the vibrational levels we had to split the nuclear motion and focus only on the interatomic distance \(r\). This means that we change the \(xyz\) coordinates into the same polar coordinates that we used for the hydrogen atom .

\[ \Psi(xyz) \rightarrow \Psi(r\theta\phi) \]

Under the harmonic and rigid rotor approximation that we will show below the radial solution (vibrational) and the angular solution (rotational) become separable.

\[ \Psi(r\theta\phi) = \Psi_{vib}(r) \Psi_{rot}(\theta\phi) \]
\[ Energy_{nuclear} = E_{vib} + E_{rot} \]

In any case the Schrodinger equation that describes the quantum rotation of a molecule is

\[ \hat{H}\Psi = \frac{\hat{L}^2}{2I}\Psi(\theta\phi) = E_{rot}\Psi(\theta\phi) \]

Where \(I\) is the moment of inertia and \(\hat{L}\) is the angular momentum operator in polar coordinates

\[ \hat{L} = -\frac{\hbar^2}{2I}\left[\frac{1}{sin\theta}\frac{\partial}{\partial\theta}\left(sin\theta\frac{\partial\Psi}{\partial\theta}\right)+ \frac{1}{sin^2\theta}\frac{\partial^2\Psi}{\partial\phi^2}\right] \]

Notice that if we consider only the angular coordinates \((\theta,\phi)\) of the system, it should remind us of the proton-electron system that we saw for the Hydrogen atom. In fact, the solutions to the angular coordinates are related to the quantum angular momentum of the system and, like in the hydrogen atom, are the Associated Legendre Polynomials.

The rigid rotor approximation#

The rigid rotor approximation assumes that the moment of inertia \(I\) is constant at all rotational levels, which is an approximation as one would expect that as the molecule rotates faster the moment of inertia is larger. This is why at higher rotational levels we would need to correct this approximation with some vibrational-rotational coupling, in a similar way that for the electron-proton there was also coupling between the angular and radial part.

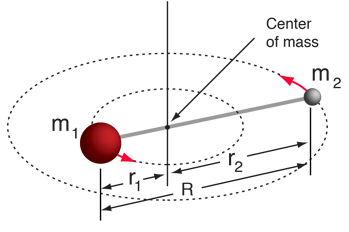
The moment of inertia of a diatomic molecule is

\[ I = m_1 r_1^2 + m_2 r_2^2 \]

or using the reduced mass \(\mu\) definition and the bond distance \(R = r_1 + r_2\)

\[ \mu = \frac{m_1 m_2}{m_1 + m_2} \]
\[ I = \mu R^2 \]

The energy levels of the rigid rotor approximation.#

The energy levels of the rigid rotor depend on the quantum number \(J=0,1,2,3...\), and its expression is

\[ E_J = \frac{\hbar^2}{2I} J(J+1) \]

The value of \(\frac{\hbar^2}{2I}\) depends on the molecular structure and it’s called the rotational constant \(B\) and it plays a similar role as the frequency in the vibrational levels. So the energy levels can be written as

\[ B = \frac{\hbar^2}{2I} \]
\[ E_J = B J(J+1) \]

Again, B is a constant for a molecule and the quantum number \(J=0,1,2,3,4...\)

Energy spacing between rotational levels#

  • What is the zero point energy for the rigid rotor system?

  • Plot the first 8 rotational levels

import matplotlib.pyplot as plt 
import numpy as np

#constants
hbar=1
#molecular properties
m1=1
m2=1
R=1

fig = plt.figure(figsize=(7,5))
ax1 = plt.subplot(111)
ax1.set_title("Rotational levels for m1="+str(m1)+" m2="+str(m2)+" R="+str(R))
ax1.set_ylabel("Rotational Energy");
_images/611ebfd8401b632b6b9bf7948f9d5b405c570a255c0086e78d252e1e6173a074.png 
import pandas as pd

rotationalTable = pd.DataFrame()

Jvalues=list(range(8))
Em1m1R1=[]
Em1m2R1=[]
rotationalTable["Eigenvalue J"] = Jvalues
for j in Jvalues:
    Em1m1R1.append(j)
    Em1m2R1.append(j)
rotationalTable["E m=1, m=1, R=1"] = Em1m1R1
rotationalTable["E m=1, m=2, R=1"] = Em1m2R1
display(rotationalTable)
Eigenvalue J E m=1, m=1, R=1 E m=1, m=2, R=1
0 0 0 0
1 1 1 1
2 2 2 2
3 3 3 3
4 4 4 4
5 5 5 5
6 6 6 6
7 7 7 7

Effect of mass#

  • Double the mass of one of the atoms to assess the effect of the mass. You may want to compare the two plots showing the energy levels next to each other.

  • How does the distribution of mass effect the rotational levels? Does the system (m1=2,m2=2) have the same rotational levels as the system (m1=1, m2=3)?

  • Besides a plot, build a table with the values.

Effect of bond distance#

  • Double the bond distance and assess the effect on rotational levels

  • Besides a plot, build a table with the values.

  • What has a larger impact on rotational levels, changes in the mass or changes in the bond distance?

  • Based on this trend, compare the rotational energy levels for N2, O2, F2, CO, NO

Degeneracy of the rigid rotor#

The quantum number \(J\) is the quantum number that appears in the eigenvalues of the angular momentum The degeneracy of the rigid rotor levels is \(2J+1\).

We say that for the rotational level J there are \(2J+1\) states. This expression should remind you of the degeneracy for the levels of the hydrogen atom. The “s” orbitals (\(\ell=0\)) had degeneracy of (\(2\cdot 0 +1 =2 \)), the “p” orbitals (\(\ell=1\)) had a degeneracy of \(2\cdot 1+1=3\), the “d” orbitals (\(\ell=2\)) had a degeneacy of \(2\cdot 2+1=5\)

The degeneracy will be important to understand in our next module the most populated states in rotational levels.

  • Build a table showing the degeneracy of the first 10 rotational levels.

Microwave spectroscopy#

Some rotational levels absorb light in the microwave region of the electromagnetic spectrum. Non-polar molecules will not absorb because they have no dipole moment. In fact, out of the three directions in which a molecule rotates, only the directions that change the direction of the dipole will absorb light. This observation is the same as the vibrational levels. Only the vibrations that change the dipole moment (in magnitude or direction) will absorb in the IR spectrum.

The rules however is that a molecule cannot “jump” from any rotational level to any other. The rules are (at this level of approximation) that it has to change by one unit

The allowed rotational transitions are:

\[ \Delta J = \pm 1 \]

  • Based on this rule, build a table showing the energy for all the possible absorptions between the first five rotational levels.

Questions#

  • Submit in a separate notebook the exercises listed above

Contents